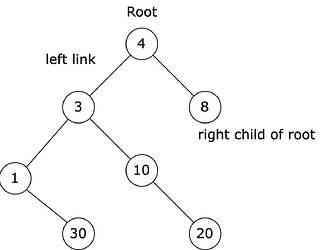
Binary search tree (BST) is a type of data structure that is commonly used to store and retrieve data efficiently. It is a tree-based data structure in which each node has at most two children, namely left and right.
The key feature of a binary search tree is that the left child of a node contains a key that is smaller than the node’s key, and the right child contains a key that is greater than or equal to the node’s key.
In this blog post, we will explore the properties of binary search trees, implementation in python, their advantages, and their disadvantages.
Properties of BST
The following properties are true for any binary search tree:
- The left subtree of a node contains only keys that are smaller than the node’s key.
- The right subtree of a node contains only keys that are greater than or equal to the node’s key.
- Both the left and right subtrees are themselves binary search trees.
Advantages of Binary Search Trees
Binary search trees have several advantages over other data structures, including:
- Efficient searching: Because of the way that binary search trees are organized, searching for a specific element in a binary search tree is very efficient. The search time is proportional to the height of the tree, which is O(log n) in the average case and O(n) in the worst case.
- Memory efficiency: Binary search trees are memory-efficient data structures because they only need to store the key values and pointers to their children.
- Easy to implement: Implementing binary search trees is relatively straightforward. The basic operations such as insertion, deletion, and searching can be implemented using simple recursive algorithms.
Disadvantages of Binary Search Trees
Despite their many advantages, binary search trees have some disadvantages as well, including:
- Unbalanced trees: If the binary search tree is unbalanced, the search time can become very inefficient. An unbalanced tree occurs when one subtree is significantly larger than the other subtree.
- Complex implementation for self-balancing: To ensure that the binary search tree remains balanced, self-balancing techniques such as AVL trees and Red-Black trees need to be implemented. These techniques can be complex and require additional memory.
Traversal
There are three common ways to traverse a binary search tree
- Inorder Traversal
- Preorder Traversal
- Postorder Traversal
Inorder traversal:
Inorder traversal is a recursive algorithm that is used to traverse a binary tree.
The algorithm starts at the root node of the binary tree and visits each node in the following order
- Traverse the left subtree by recursively calling the inorder function on the left child node.
- Visit the current node.
- Traverse the right subtree by recursively calling the inorder function on the right child node.
In other words, the inorder traversal algorithm first visits all the nodes in the left subtree, then visits the current node, and finally visits all the nodes in the right subtree.
The inorder traversal algorithm is called “inorder” because it visits the nodes in the order in which they would be visited if the binary tree were printed out in order. That is, if the binary tree represents a sorted list of values, then the inorder traversal algorithm would visit the nodes in the order of the sorted list.
Preorder traversal
Preorder traversal is a recursive algorithm that is used to traverse a binary tree. The algorithm starts at the root node of the binary tree and visits each node in the following order:
- Visit the current node.
- Traverse the left subtree by recursively calling the preorder function on the left child node.
- Traverse the right subtree by recursively calling the preorder function on the right child node.
In other words, the preorder traversal algorithm first visits the current node, then visits all the nodes in the left subtree, and finally visits all the nodes in the right subtree.
The preorder traversal algorithm is called “preorder” because it visits the nodes in the order in which they would be visited if the binary tree were printed out in preorder. That is, the value of the root node is printed first, followed by the values of all nodes in the left subtree, and finally followed by the values of all nodes in the right subtree.
Postorder traversal.
Postorder traversal is a recursive algorithm that is used to traverse a binary tree. The algorithm starts at the root node of the binary tree and visits each node in the following order:
- Traverse the left subtree by recursively calling the postorder function on the left child node.
- Traverse the right subtree by recursively calling the postorder function on the right child node.
- Visit the current node.
In other words, the postorder traversal algorithm first visits all the nodes in the left subtree, then visits all the nodes in the right subtree, and finally visits the current node.
The postorder traversal algorithm is called “postorder” because it visits the nodes in the order in which they would be visited if the binary tree were printed out in postorder. That is, the values of all nodes in the left subtree are printed first, followed by the values of all nodes in the right subtree, and finally followed by the value of the root node.
Python Implementation of BST
Here is an implementation of all three traversal methods for a binary search tree:
from typing import Any, List, Optional
class Node:
"""A node in a Binary Search Tree (BST).
Attributes:
value: The value of the node.
left: The left child node.
right: The right child node.
"""
def __init__(self, value: Any):
self.value = value
self.left_child = None
self.right_child = None
class BinarySearchTree:
"""A Binary Search Tree (BST).
Attributes:
root: The root node of the BST.
"""
def __init__(self):
self.root = None
def insert(self, value: Any) -> None:
"""Inserts a node with a given value into the BST.
Args:
value: The value of the node to insert.
"""
if not self.root:
self.root = Node(value)
else:
self._insert(value, self.root)
def _insert(self, value: Any, current_node: Node) -> None:
"""Inserts a node with a given value into the BST.
Args:
value: The value of the node to insert.
"""
if value < current_node.value:
if not current_node.left_child:
current_node.left_child = Node(value)
else:
self._insert(value, current_node.left_child)
elif value > current_node.value:
if not current_node.right_child:
current_node.right_child = Node(value)
else:
self._insert(value, current_node.right_child)
else:
print("Value already in tree.")
def inorder_traversal(self) -> List[Any]:
"""Returns a list of values of the nodes in the BST using inorder traversal.
Returns:
A list of values of the nodes in the BST using inorder traversal.
"""
return self._inorder_traversal(self.root, [])
def _inorder_traversal(self, current_node: None, result: List[Any]) -> List[Any]:
"""Returns a list of values of the nodes in the BST using inorder traversal.
Args:
current_node: The current node being traversed.
result: Traversed nodes.
Returns:
A list of values of the nodes in the BST using inorder traversal.
"""
if not current_node:
return result
self._inorder_traversal(current_node.left_child, result)
result.append(current_node.value)
self._inorder_traversal(current_node.right_child, result)
return result
def preorder_traversal(self):
"""Returns a list of values of the nodes in the BST using preorder traversal.
Returns:
A list of values of the nodes in the BST using preorder traversal.
"""
return self._preorder_traversal(self.root, [])
def _preorder_traversal(self, current_node, result):
"""Returns a list of values of the nodes in the BST using preorder traversal.
Args:
current_node: The current node being traversed.
result: Traversed nodes.
Returns:
A list of values of the nodes in the BST using preorder traversal.
"""
if not current_node:
return result
result.append(current_node.value)
self._preorder_traversal(current_node.left_child, result)
self._preorder_traversal(current_node.right_child, result)
return result
def postorder_traversal(self):
"""Returns a list of values of the nodes in the BST using postorder traversal.
Returns:
A list of values of the nodes in the BST using postorder traversal.
"""
return self._postorder_traversal(self.root, [])
def _postorder_traversal(self, current_node, result):
"""Returns a list of values of the nodes in the BST using postorder traversal.
Args:
current_node: The current node being traversed.
result: Traversed nodes.
Returns:
A list of values of the nodes in the BST using postorder traversal.
"""
if not current_node:
return result
self._postorder_traversal(current_node.left_child, result)
self._postorder_traversal(current_node.right_child, result)
result.append(current_node.value)
return result
def _delete(self, node: Node, value: Any) -> Optional[Node]:
"""Recursively deletes a node with a given value from the BST.
Args:
node: The current node being traversed.
value: The value of the node to delete.
Returns:
The node to be deleted or None if it is not found.
"""
if node is None:
return None
elif value < node.value:
node.left_child = self._delete(node.left_child, value)
elif value > node.value:
node.right_child = self._delete(node.right_child, value)
else:
if node.left_child is None and node.right_child is None:
node = None
elif node.left_child is None:
node = node.right_child
elif node.right_child is None:
node = node.left_child
else:
min_node = self._find_min(node.right_child)
node.value = min_node.value
node.right_child = self._delete(node.right_child, min_node.value)
return node
def delete(self, value: int) -> None:
"""Deletes a node with a given value from the BST.
Args:
value: The value of the node to delete.
"""
self.root = self._delete(self.root, value)
def _find_min(self, node: Node) -> Node:
"""Returns the node with the minimum value in the BST.
Args:
node: The current node being traversed.
Returns:
The node with the minimum value in the BST.
"""
while node.left is not None:
node = node.left
return node
if __name__ == "__main__":
tree = BinarySearchTree()
tree.insert(15)
tree.insert(3)
tree.insert(9)
tree.insert(10)
tree.insert(2)
tree.insert(4)
tree.insert(7)
print(tree.inorder_traversal())
print(tree.preorder_traversal())
print(tree.postorder_traversal())
tree.delete(4)
print(tree.inorder_traversal())
tree.delete(10)
print(tree.inorder_traversal())
tree.delete(15)
print(tree.inorder_traversal())
In this implementation, the inorder_traversal method traverses the tree in left-root-right order, the preorder_traversal method traverses the tree in root-left-right order, and the postorder_traversal method traverses the tree in left-right-root order. All three methods take a current_node and a result list as arguments and use recursion to traverse the tree.
The _inorder_traversal method first recursively traverses the left subtree of the current node, then appends the current node’s value to the result list, and finally recursively traverses the right subtree of the current node.
The _preorder_traversal method first appends the current node’s value to the result list, then recursively traverses the left subtree of the current node, and finally recursively traverses the right subtree of the current node.
The _postorder_traversal method traverse the left subtree, then the right subtree, and finally print the root node’s value.
BST node deletion
To delete a node from a Binary Search Tree (BST), you need to perform the following steps:
- Find the node to be deleted.
- Start at the root of the BST.
- If the node to be deleted is less than the current node, move to the left child.
- If the node to be deleted is greater than the current node, move to the right child.
- Repeat until the node to be deleted is found or we reach a null node.
- Delete the node.
- If the node to be deleted has no children, simply remove it from the tree.
- If the node to be deleted has one child, replace it with its child.
- If the node to be deleted has two children, replace it with the minimum value node from its right subtree.
- Update the BST
- If the node to be deleted is the root, update the root.
- If the node to be deleted is a left child, update its parent’s left child.
- If the node to be deleted is a right child, update its parent’s right child.
Note that the _delete method is a recursive method that takes a node and a value as inputs. It returns the node to be deleted or None if it is not found. If the node is found, it performs the deletion process as described above and returns the updated node. The self._find_min method is a helper method that finds the minimum value node in the right subtree of the node to be deleted.