Divide and conquer is a popular problem-solving technique in computer science and mathematics. It involves breaking down a complex problem into smaller sub-problems, solving each sub-problem independently, and then combining the solutions to the sub-problems to solve the original problem.
In this blog post, we will explore the divide and conquer algorithm in more detail, including its benefits, applications, and some examples.
Divide and conquer algorithm basics
The divide and conquer algorithm can be broken down into three basic steps:
- Divide: The first step involves dividing the problem into smaller sub-problems that are similar to the original problem, but smaller in size. This can be achieved by breaking the problem down into smaller chunks or by dividing the problem into sub-problems based on some other criteria.
- Conquer: The second step involves solving the sub-problems independently. This can be achieved by applying the same divide and conquer algorithm recursively until the sub-problems become simple enough to be solved directly.
- Combine: The final step involves combining the solutions to the sub-problems to solve the original problem. This can be achieved by merging the solutions, selecting the best solution, or applying some other combination method.
Advantages:
- Efficiency: Divide and conquer algorithms are often highly efficient, especially for large input sizes, since they can break down a problem into smaller subproblems that can be solved independently and in parallel.
- Scalability: As the input size grows, divide and conquer algorithms scale well since they can handle larger problems by recursively breaking them down into smaller subproblems.
- Modularization: The divide and conquer approach naturally lends itself to modular programming, since it breaks down a problem into smaller, more manageable subproblems that can be solved independently.
- Parallelization: Divide and conquer algorithms can be easily parallelized, since each subproblem can be solved independently and in parallel.
Disadvantages:
- Overhead: The overhead of the divide and conquer approach can be significant, especially for small input sizes, since it involves breaking down the problem into smaller subproblems and then combining the results.
- Recursion: The divide and conquer approach often involves recursion, which can be less efficient than iterative solutions due to the overhead of function calls and memory usage.
- Unbalanced Subproblems: In some cases, the divide and conquer approach can lead to unbalanced subproblems, which can result in poor performance if one subproblem takes significantly longer to solve than the others.
- Difficulty: Developing an efficient divide and conquer algorithm requires a deep understanding of the problem and the ability to break it down into smaller subproblems, which can be challenging for some problems.
Binary Search using Divide and Conquer
from typing import List
def binary_search(arr: List[int], target: int) -> int:
"""Searches for a target element in a sorted list using the binary search algorithm.
Args:
arr: A sorted list of integers.
target: The integer to search for in the list.
Returns:
The index of the target element in the list if found, or -1 otherwise.
"""
# Initialize the starting and ending indices
start = 0
end = len(arr) - 1
# Keep searching while the start index is less than or equal to the end index
while start <= end:
# Calculate the middle index
mid = (start + end) // 2
# If the middle element is the target, return its index
if arr[mid] == target:
return mid
# If the middle element is less than the target, search the right half of the list
elif arr[mid] < target:
start = mid + 1
# If the middle element is greater than the target, search the left half of the list
else:
end = mid - 1
# If the target is not found, return -1
return -1
a = [1, 2, 3, 4, 9, 20, 23]
print(binary_search(a, 1))
print(binary_search(a, 20))
print(binary_search(a, 23))
print(binary_search(a, 0))
In the above code, we implement the binary search algorithm using the divide and conquer approach. We start by initializing the starting and ending indices of the list, and then we keep searching for the target element by dividing the list in half and recursively searching either the left or right half of the list based on the comparison with the middle element.
How to approach a problem using Divide and Conquer
The divide and conquer algorithmic approach is suitable for solving problems that can be broken down into smaller, independent subproblems that are similar in structure to the original problem. Here are some steps you can follow to determine if you can use the divide and conquer approach to solve a problem:
- Identify the problem: First, you need to understand the problem and identify its characteristics and constraints.
- Analyze the problem: Next, you need to analyze the problem and determine if it can be broken down into smaller subproblems that are similar in structure to the original problem.
- Identify the subproblems: Once you have identified the subproblems, you need to determine how to solve them independently.
- Combine the solutions: Finally, you need to combine the solutions to the subproblems to obtain the solution to the original problem.
If the problem can be broken down into smaller subproblems that are similar in structure to the original problem and the solutions to the subproblems can be combined to obtain the solution to the original problem, then the divide and conquer approach is a suitable algorithmic technique to use.
However, not all problems can be solved using the divide and conquer approach. Some problems may be too complex or may not have a clear structure that can be broken down into smaller subproblems. In such cases, other algorithmic approaches may be more suitable, such as dynamic programming or greedy algorithms.
Example explanation
Let’s consider an example of using the divide and conquer approach to sort a list of numbers using the merge sort algorithm.
The merge sort algorithm uses the following steps:
- Divide the list into two halves.
- Recursively sort each half.
- Merge the sorted halves into a single sorted list.
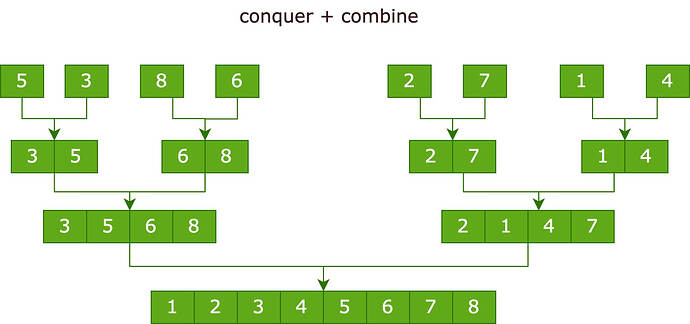
For example, consider the following list of numbers: [5, 3, 8, 6, 2, 7, 1, 4]
- Divide the list into two halves: [5, 3, 8, 6] and [2, 7, 1, 4]
- Recursively sort each half:
For the first half: [5, 3, 8, 6]
Divide the first half into two halves: [5, 3] and [8, 6]
Recursively sort each half:
For the first half: [5, 3]
Divide the first half into two halves: [5] and [3]
The subproblem of sorting [5] and [3] is trivial since they are already sorted.
Merge the sorted halves [5] and [3] into a single sorted list [3, 5]
For the second half: [8, 6]
Divide the second half into two halves: [8] and [6]
The subproblem of sorting [8] and [6] is trivial since they are already sorted
Merge the sorted halves [8] and [6] into a single sorted list [6, 8]
Merge the sorted halves [3, 5] and [6, 8] into a single sorted list [3, 5, 6, 8].
For the second half: [2, 7, 1, 4]
Divide the second half into two halves: [2, 7] and [1, 4]
Recursively sort each half:
For the first half: [2, 7]
Divide the first half into two halves: [2] and [7]
The subproblem of sorting [2] and [7] is trivial since they are already sorted.
Merge the sorted halves [2] and [7] into a single sorted list [2, 7].
For the second half: [1, 4]
Divide the second half into two halves: [1] and [4]
The subproblem of sorting [1] and [4] is trivial since they are already sorted.
Merge the sorted halves [1] and [4] into a single sorted list [1, 4].
Merge the sorted halves [2, 7] and [1, 4] into a single sorted list [1, 2, 4, 7].
Merge the sorted halves [3, 5, 6, 8] and [1, 2, 4, 7] into a single sorted list [1, 2, 3, 4, 5, 6, 7, 8].
The above example demonstrates how the divide and conquer approach can be used to solve a problem, in this case, sorting a list of numbers using the merge sort algorithm. By breaking down the problem into smaller