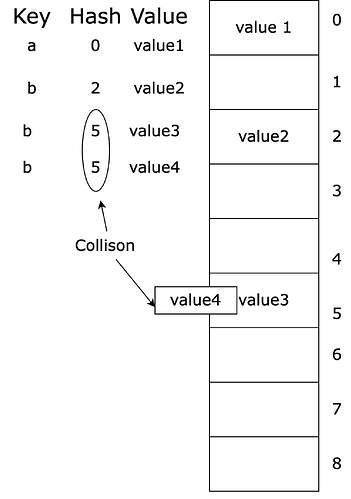
The hash table is a key value store data structure.
Hash tables are a fundamental data structure in computer science that allows for efficient storage and retrieval of data. A hash table, also known as a hash map, is a collection of key-value pairs, where each key is mapped to a unique index in an array using a hash function.
Hash Table is designed for efficient data retrieval, search and insertion. It exploits the unique advantages of the array data structure. Hash tables are implemented using an array as the backend.
The array supports constant time insertion and access, which makes it very suitable for application that needs fast insertion and retrieval.
Key: Each entry in the table has unique Keys. The key should be of a hashable type.
Value: Value corresponding to the key. It can be any type.
The advantage of using a hash table is that it provides constant-time lookup, insertion, and deletion of elements, on average. This makes it a powerful data structure for implementing algorithms that require quick data access, such as database indexing or symbol tables.
One common application of hash tables is in programming languages, where they are used to implement dictionaries or associative arrays. For example, Python’s built-in dictionary type uses a hash table to provide a constant-time lookup of key-value pairs.
Another application of hash tables is in cryptography, where they are used to implement hash functions. Hash functions take an input message of arbitrary length and produce a fixed-size output called a hash, which can be used to verify the integrity of data.
Despite its many advantages, hash tables do have some limitations. One limitation is that the hash function can be a source of security vulnerabilities, as attackers can exploit weaknesses in the function to cause collisions and potentially gain unauthorized access to data. Additionally, hash tables may not perform well when the load factor, or the ratio of elements to the size of the array, becomes too high, leading to increased collisions and decreased performance.
In conclusion, hash tables are a powerful and widely used data structure in computer science, with applications ranging from programming languages to cryptography. While they have some limitations, their constant-time lookup, insertion, and deletion make them valuable tools for optimizing performance in various algorithms and applications.
Hashing
To retrieve an element or insert an element into an array we need the index of that element in the array. To get the index, the key of the hash table is hashed using a hash function. This process is also called hashing and is very crucial for the efficient design of the Hash Table.
The hash function takes the key as input and produces an index in the array.
The hash function takes the key as an input and produces an index. An ideal hash function has the following characteristics:
- Efficient runtime: It should be simple and fast.
- Uniform distribution: It should map the keys into a uniform distribution such that all indices are used. It should avoid mapping multiple keys into the same index.
- Fewer collisions: Collisions should be avoided. Frequent collisions result in a slow and inefficient hash table.
DJB2 hashing algorithm
DJB2 hashing algorithm, which is a simple and fast hash function that is commonly used in hash tables. It computes a hash value by iterating over each character in the input string, multiplying the current hash value by 31, adding the ASCII value of the character, and taking the result modulo 2^32.
Note that the modulo operation is used to ensure that the hash value fits within a certain range, which is important for hash table implementations that use an array to store key-value pairs. In practice, the size of the hash table should be chosen to be a prime number to reduce the likelihood of collisions.
Overall, this implementation provides a basic hashing function in Python that can be used for simple applications. However, for more complex applications, it may be necessary to use a more sophisticated hashing function that provides better distribution and collision resistance.
def djb2_hash(s):
hash_value = 0
for c in s:
hash_value = (hash_value * 31 + ord(c)) % (2**32)
return hash_value
Collisions
Ideally, the hash function should produce a unique index for each key, but in reality, collisions can occur when two different keys are mapped to the same index. To handle collisions, various techniques such as separate chaining or open addressing can be used.
Ideally, we should attempt to design a collision-free hash function. But in practice, it becomes very difficult to have a collision-free function. A certain level of collision is acceptable as long as it does not form visible clusters.
When there is a collision, values of all those keys with the same index should be placed in that index. But we can not insert more than one value in the same index. So when collisions occur we need to use collision resolution methods. Collision resolution methods introduce additional computation and memory overheads.
Collisions can be resolved using the following methods:
- Chaining based collisions resolution
- Open addressing
Separate Chaining Collision resolution
A hash function transforms keys into array indices, but when multiple keys map to the same index, collision resolution becomes necessary. This involves determining how to handle the situation when two or more keys need to be inserted into the same index. One common approach to collision resolution is to construct linked lists of key-value pairs for each of the M array indices. Each linked list contains pairs whose keys hash to the same index. To ensure efficient search, M is chosen to be sufficiently large, such that the lists are short enough to enable a two-step process: first, locate the list that could contain the key by hashing, and then search sequentially through that list for the key.
Open addressing Collision resolution
An alternative method for implementing hashing involves using a hash table of size M, which is greater than the number of N key-value pairs that need to be stored. This approach relies on empty slots in the table to aid in resolving collisions and is known as open-addressing hashing. Linear probing is the most basic form of open-addressing hashing: when a collision occurs (i.e., when a key hashes to an index in the table that is already occupied by a different key), the algorithm proceeds to check the next entry in the table by incrementing the index.
Implementations of a Hash Table or Hash Map in Python
Separate Chaining Hash Table Implementation
from typing import Any, List, Optional, Tuple
class Node:
"""A node class to be used for linked lists in separate chaining.
Attributes:
key: The key of the node.
value: The value associated with the key.
next: A reference to the next node in the linked list.
"""
def __init__(self, key: Any, value: Any) -> None:
"""
Initializes a node.
Args:
key: The key of the node.
value: The value associated with the key.
"""
self.key: Any = key
self.value: Any = value
self.next: Optional[Node] = None
class HashTable:
"""A hash table implementation using separate chaining collision resolution.
Attributes:
Attributes:
table: A list of key-value pairs representing the hash table.
size: The size of the hash table.
capacity: The maximum number of key-value pairs the hash table can hold.
load_factor: The maximum ratio of size to capacity before the table is resized.
"""
def __init__(self, capacity: int = 1000, load_factor: float = 0.75) -> None:
"""Initializes the hash table.
Args:
capacity: The maximum number of key-value pairs the hash table can hold.
load_factor: The maximum ratio of size to capacity before the table is resized.
"""
self.table: List[Optional[Node]] = [None] * capacity
self.size: int = 0
self.capacity: int = capacity
self.load_factor: float = load_factor
def _hash(self, key: Any) -> int:
"""Calculates the hash value of a key.
Args:
key: The key to hash.
Returns:
The hash value of the key.
"""
return hash(key) % self.capacity
def _resize(self) -> None:
"""Resizes the hash table by creating a new table with twice the capacity and
rehashing all the key-value pairs.
"""
new_capacity: int = int(self.capacity * 2)
new_table: List[Optional[Node]] = [None] * new_capacity
self.capacity = new_capacity
for node in self.table:
while node is not None:
hash_value: int = self._hash(node.key)
if new_table[hash_value] is None:
new_table[hash_value] = Node(node.key, node.value)
else:
new_node: Node = Node(node.key, node.value)
new_node.next = new_table[hash_value]
new_table[hash_value] = new_node
node = node.next
self.table = new_table
def put(self, key: Any, value: Any) -> None:
"""Adds a key-value pair to the hash table.
Args:
key: The key of the key-value pair.
value: The value of the key-value pair.
"""
if self.size >= self.capacity * self.load_factor:
self._resize()
hash_value: int = self._hash(key)
if self.table[hash_value] is None:
self.table[hash_value] = Node(key, value)
else:
node: Optional[Node] = self.table[hash_value]
while node is not None:
if node.key == key:
node.value = value
return
node = node.next
new_node: Node = Node(key, value)
new_node.next = self.table[hash_value]
self.table[hash_value] = new_node
self.size += 1
def get(self, key: Any) -> Optional[Any]:
"""Retrieves the value associated with a key.
Args:
key: The key to retrieve the value for.
Returns:
The value associated with the key, or None if the key is not found.
"""
hash_value: int = self._hash(key)
node: Optional[Node] = self.table[hash_value]
while node is not None:
if node.key == key:
return node.value
node = node.next
return None
if __name__ == "__main__":
simple_map = HashTable(capacity=10)
for i in range(9):
simple_map.put("key_" + str(i), i)
print(simple_map.capacity)
for i in range(9, 20):
simple_map.put("key_"+ str(i), i)
print(simple_map.capacity)
for i in range(20):
print(simple_map.get("key_" + str(i)))
Here, we define a Node class to hold the key-value pairs and a HashTable class that initializes an empty array of a specified size. We also define a hash function that uses Python’s built-in hash() function to generate an index for each key.
To insert a key-value pair, we first calculate the index using the hash function. If the index is empty, we simply create a new node with the key-value pair. If the index is not empty, we traverse the linked list at that index to find the end and append a new node.
To search for a key, we calculate the index and traverse the linked list at that index until we find the key or reach the end of the list. If the key is found, we return the corresponding value. If not, we return None.
To delete a key-value pair, we calculate the index and traverse the linked list at that index until we find the key or reach the end of the list. If the key is found, we remove the corresponding node from the linked list. If not, we return False.
This is just one implementation of a hash table in Python, and there are many variations and optimizations that can be made depending on the specific use case.
Open Addressing Hash Table Implementation
from typing import Any, List, Optional, Tuple
class HashTable:
"""A hash table implementation using open addressing collision resolution.
Attributes:
table: A list of key-value pairs representing the hash table.
size: The size of the hash table.
capacity: The maximum number of key-value pairs the hash table can hold.
"""
def __init__(self, capacity: int = 1000) -> None:
"""Initializes the hash table.
Args:
capacity: The maximum number of key-value pairs the hash table can hold.
Defaults to 1000.
"""
self.table: List[Optional[Tuple[Any, Any]]] = [None] * capacity
self.size: int = 0
self.capacity: int = capacity
def _hash(self, key: Any) -> int:
"""Calculates the hash value of a key.
Args:
key: The key to hash.
Returns:
The hash value of the key.
"""
return hash(key) % self.capacity
def _rehash(self, old_hash: int) -> int:
"""Finds the next available hash value using linear probing.
Args:
old_hash: The original hash value.
Returns:
The next available hash value.
"""
return (old_hash + 1) % self.capacity
def put(self, key: Any, value: Any) -> None:
"""Adds a key-value pair to the hash table.
Args:
key: The key of the key-value pair.
value: The value of the key-value pair.
"""
hash_value: int = self._hash(key)
while self.table[hash_value] is not None and self.table[hash_value][0] != key:
hash_value = self._rehash(hash_value)
if self.table[hash_value] is None:
self.size += 1
self.table[hash_value] = (key, value)
print(f"hash: {hash_value}, key: {key}, value:{value}")
if self.size >= self.capacity * 0.75:
self._resize()
def get(self, key: Any) -> Optional[Any]:
"""Retrieves the value associated with a key.
Args:
key: The key to retrieve the value for.
Returns:
The value associated with the key, or None if the key is not found.
"""
hash_value: int = self._hash(key)
while self.table[hash_value] is not None and self.table[hash_value][0] != key:
hash_value = self._rehash(hash_value)
if self.table[hash_value] is None:
return None
else:
return self.table[hash_value][1]
def _resize(self) -> None:
"""Resizes the hash table when the load factor exceeds 0.75."""
new_capacity: int = self.capacity * 2
old_capacity = self.capacity
self.capacity = new_capacity
print(f"old: {old_capacity}")
new_table: List[Optional[Tuple[Any, Any]]] = [None] * self.capacity
for i in range(old_capacity):
if self.table[i] is not None:
key, value = self.table[i]
hash_value: int = hash(key) % self.capacity
while new_table[hash_value] is not None:
hash_value = self._rehash(hash_value)
new_table[hash_value] = (key, value)
self.table = new_table
if __name__ == "__main__":
simple_map = HashTable(capacity=10)
for i in range(9):
simple_map.put("key_" + str(i), i)
print(simple_map.capacity)
print(simple_map.table)
for i in range(9, 20):
simple_map.put("key_"+ str(i), i)
print(simple_map.capacity)
print(simple_map.table)
print(simple_map.table)
for i in range(20):
print(simple_map.get("key_" + str(i)))
This implementation uses a list of tuples, each tuple containing a key and value for each entry. The hash function is used to compute the index in the list for a given key.
The put function adds a key-value pair to the hash table, while the get function retrieves the value associated with a key. If the key is not in the hash table, None is returned. The remove function removes a key-value pair from the hash table.
In order to handle collisions, this implementation uses open addressing, which means that if the computed index is already occupied, it simply tries the next index until it finds an empty slot. This can lead to clustering, which can cause performance issues if the hash table becomes too full.
Overall, this implementation provides a basic hash table using open addressing for collision resolution. However, for larger or more complex applications, it may be necessary to use a more sophisticated hash table implementation.