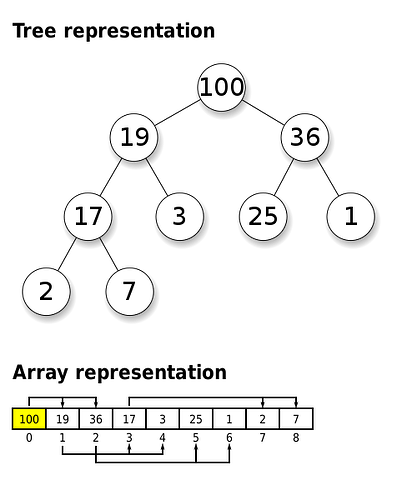
Heap
When it comes to data structures, the heap is a powerful and versatile one that plays a crucial role in
computer science and programming.
Heaps are a specialized tree-based data structure that satisfies the “heap” property - the value of a node is greater than or equal to (or less than) the values of its children. Heaps have an array-based implementation and provide efficient O(log n) insertion and removal.
What is a Heap?
A heap is a binary tree-based data structure that can be visualized as a tree where each node has one or more child nodes. The heap property distinguishes it from a regular binary tree. Depending on the type of heap, this property can take two forms:
Heap Property
- Min-Heap : In a min-heap, for any given node ‘N,’ the value of ‘N’ is less than or equal to the values of its children. This means the smallest element is at the root.
- Max-Heap : In a max-heap, for any given node ‘N,’ the value of ‘N’ is greater than or equal to the values of its children. This means the largest element is at the root.
Why Use a Heap?
The heap is fundamentally a priority queue - it always keeps track of the maximum or minimum value. The root node contains the highest (or lowest) priority element.
This provides several benefits:
- Efficient removals - The max/min element can always be removed in
O(log n)time. Useful for scheduling algorithms. - Order statistics - Heaps are used to efficiently find the
kthsmallest/largest element in an array. - Heapsort - An efficient
O(n log n)sorting algorithm can be designed using heaps.
Heaps provide fast access to the highest priority element without needing to maintain a sorted order.
Heap Operations
Heaps support a few essential operations that make them valuable in various algorithms:
1. Insertion
- To insert an element into a heap, you add it to the last available position in the tree.
- Then, you need to maintain the heap property by performing a process called “heapify-up” or “bubble-up,” which involves comparing the element with its parent and swapping them if necessary until the heap property is restored.
2. Remove / Extraction
- To extract the minimum (in a min-heap) or maximum (in a max-heap) element from a heap, you typically remove the root node.
- To maintain the heap property after extraction, you replace the root with the last node in the tree.
- Then, you perform a process called “heapify-down” or “bubble-down,” where you compare the new root with its children and swap it with the smaller (in a min-heap) or larger (in a max-heap) child until the heap property is restored.
3. Access
- You can access the minimum or maximum element of a heap without removing it by simply looking at the root node.
The key operations and their time complexities are:
* Access max/min - O(1)
* Insert - O(log n)
* Remove max/min - O(log n)
* Build heap - O(n) time from an unordered array
Heaps provide efficient inserts and removals while maintaining easy access to the extremum element. This makes them useful as priority queues in applications like schedulers and graph algorithms.
Implementation in Arrays
Heaps are complete binary trees, meaning they are filled level by level and only the deepest level may be partially filled.
We can therefore represent them compactly in arrays, using the formula:
- Parent at index
(i - 1) / 2 - Left child at index
2i + 1 - Right child at index
2i + 2
Insertion and removal can be implemented by swapping elements and “bubbling” them up or down until the heap property is restored.
Python implementation of the Heap data structure
from typing import List, Optional
class MinHeap:
"""A class representing a min-heap data structure.
To utilize it as a max-heap data structure, insert the negation
(or negative counterparts) of the values you wish to use.
"""
def __init__(self) -> None:
"""Initializes an empty min-heap."""
self.heap: List[int] = []
self.size: int = 0
def parent(self, i: int) -> int:
"""Get the index of the parent node of a node at index i.
Args:
i: The index of the node.
Returns:
The index of the parent node.
"""
return (i - 1) // 2
def left_child(self, i: int) -> int:
"""Get the index of the left child of a node at index i.
Args:
i: The index of the node.
Returns:
The index of the left child node.
"""
return 2 * i + 1
def right_child(self, i: int) -> int:
"""Get the index of the right child of a node at index i.
Args:
i: The index of the node.
Returns:
The index of the right child node.
"""
return 2 * i + 2
def insert(self, key: int) -> None:
"""Insert a key into the min-heap.
Args:
key: The key to be inserted.
"""
self.heap.append(key)
self.size += 1
self._heapify_up(self.size - 1)
def extract_min(self) -> Optional[int]:
"""Extract and return the minimum element from the min-heap.
Returns:
The minimum element or None if the heap is empty.
"""
if self.size == 0:
return None
if self.size == 1:
self.size -= 1
return self.heap.pop()
root = self.heap[0]
self.heap[0] = self.heap.pop()
self.size -= 1
self._heapify_down(0)
return root
def _heapify_up(self, i: int) -> None:
"""Restore the heap property by moving a node up the tree.
Args:
i: The index of the node to be moved up.
"""
while i > 0 and self.heap[i] < self.heap[self.parent(i)]:
self.heap[i], self.heap[self.parent(i)] = self.heap[self.parent(i)], self.heap[i]
i = self.parent(i)
def _heapify_down(self, i: int) -> None:
"""Restore the heap property by moving a node down the tree.
Args:
i: The index of the node to be moved down.
"""
smallest = i
left = self.left_child(i)
right = self.right_child(i)
if left < self.size and self.heap[left] < self.heap[smallest]:
smallest = left
if right < self.size and self.heap[right] < self.heap[smallest]:
smallest = right
if smallest != i:
self.heap[i], self.heap[smallest] = self.heap[smallest], self.heap[i]
self._heapify_down(smallest)
def get_min(self) -> Optional[int]:
"""Get the minimum element from the min-heap without removing it.
Returns:
The minimum element or None if the heap is empty.
"""
return None if self.size == 0 else self.heap[0]
def is_empty(self) -> bool:
"""Check if the min-heap is empty.
Returns:
True if the heap is empty, False otherwise.
"""
return self.size == 0
def heapify(self, arr: List[int]) -> None:
"""Convert an array into a valid min-heap.
Args:
arr: The list of elements to be converted into a heap.
"""
self.size = len(arr)
self.heap = arr
for i in range(self.size // 2 - 1, -1, -1):
self._heapify_down(i)
# Example:
if __name__ == "__main__":
min_heap = MinHeap()
min_heap.insert(4)
min_heap.insert(9)
min_heap.insert(2)
min_heap.insert(1)
min_heap.insert(5)
print(f"Min heap: {min_heap.heap}")
min_element = min_heap.extract_min()
print(f"Extracted minimum element: {min_element}")
print(f"Min heap after extraction: {min_heap.heap}")
print(f"Minimum element without extraction: {min_heap.get_min()}")
print("Max Heap")
max_heap = MinHeap()
max_heap.insert(-4)
max_heap.insert(-9)
max_heap.insert(-2)
max_heap.insert(-1)
max_heap.insert(-5)
print(f"Max heap: {max_heap.heap}")
max_element = - max_heap.extract_min()
print(f"Extracted maximum element: {max_element}")
print(f"Max heap after extraction: {max_heap.heap}")
print(f"Maximum element without extraction: {-max_heap.get_min()}")
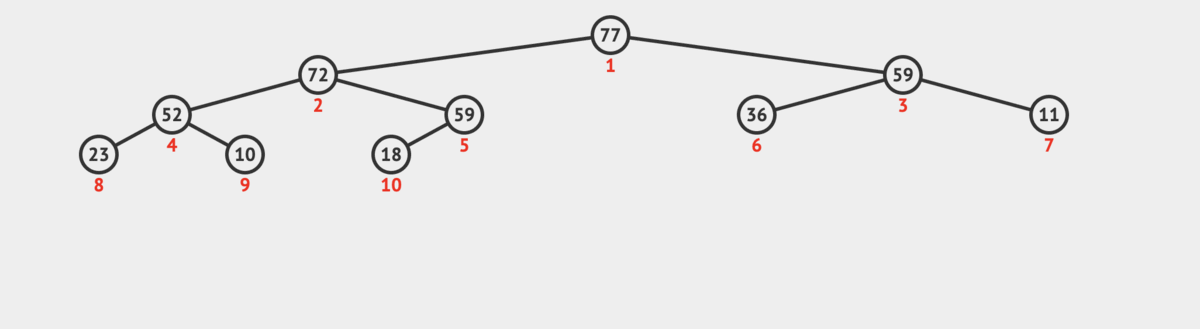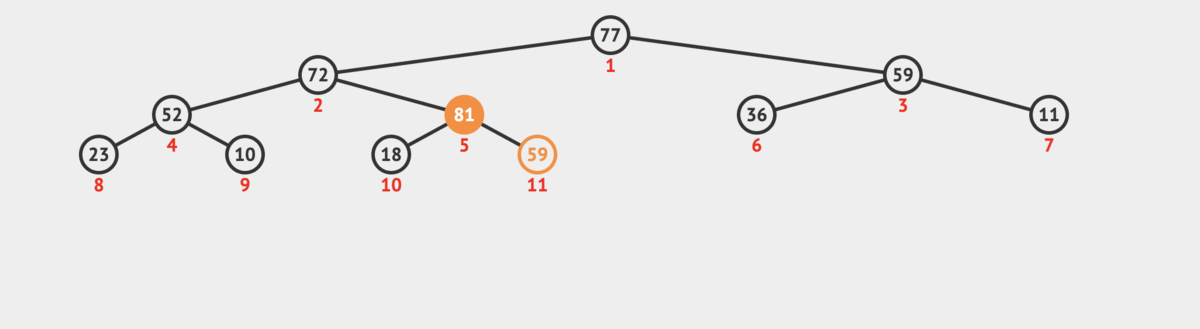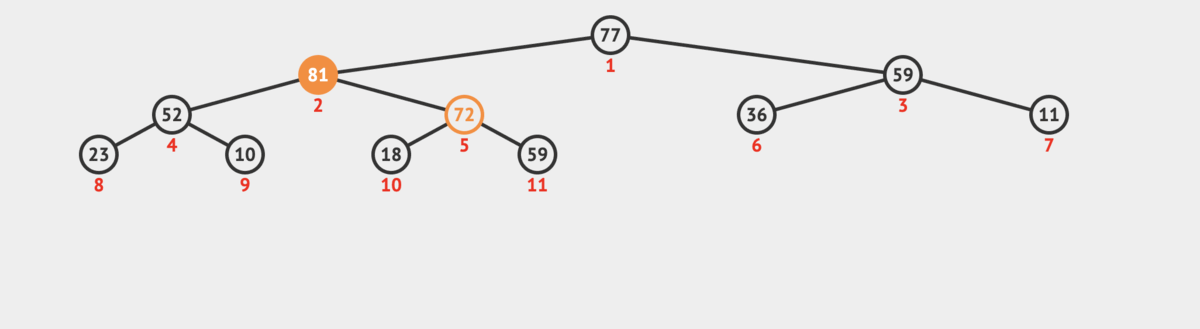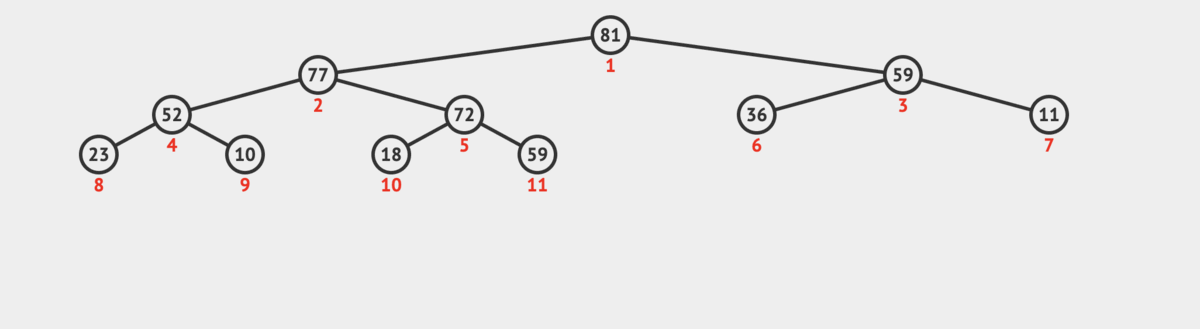
Insert explanation
The heap insertion algorithm allows us to insert a new element into a max heap while maintaining the heap property.
The steps are:
- Add the new element to the end of the heap array.
- Heapify up the element to its proper position:
- Compare the new element to its parent node
- If it is greater than its parent (in a max heap), swap the two elements
- Repeat this process until the heap property is satisfied
The Heapify up operation flows up the heap comparing the new element against its parent and swapping if necessary.
- Once the element is greater than its parent or becomes the root, the heap property is satisfied.
The insertion completes in O(log n) time since in the worst case, we bubble/heapify up from the bottom level of the heap to the root.
Remove explanation
The heap removal algorithm allows us to delete the maximum element from a max heap while maintaining the heap property.
The steps are:
-
Store the max element to return later and replace it with the last element in the heap.
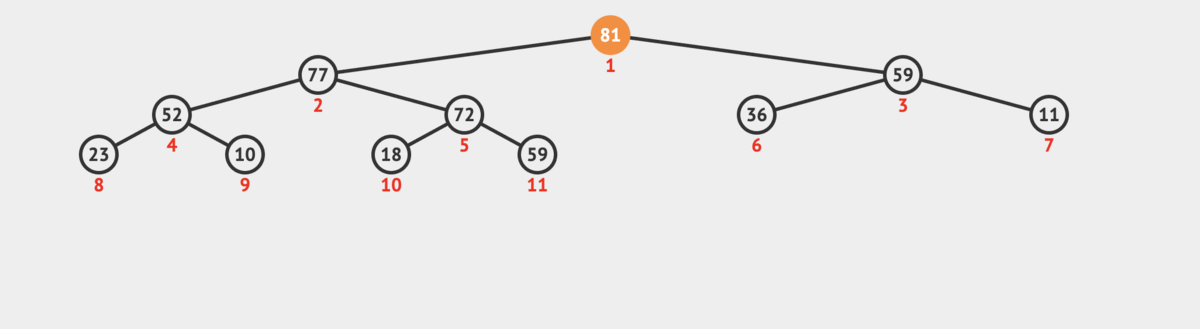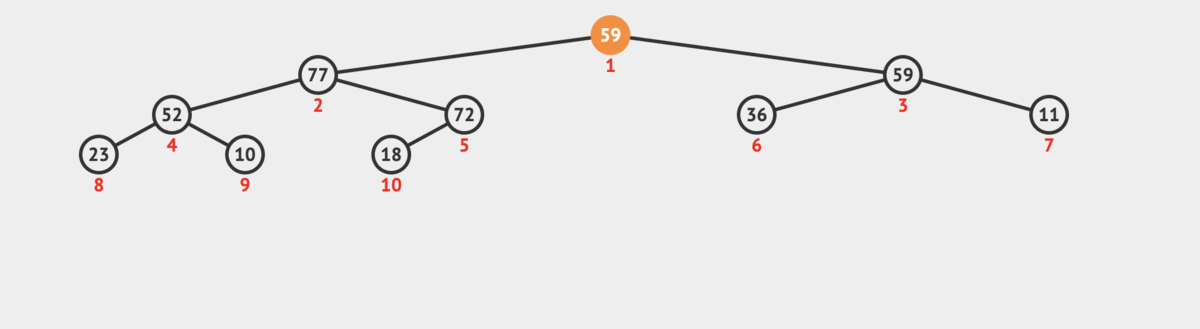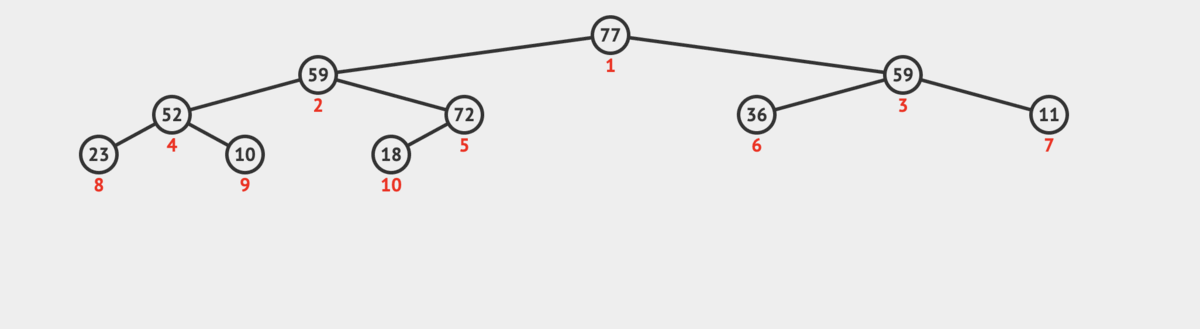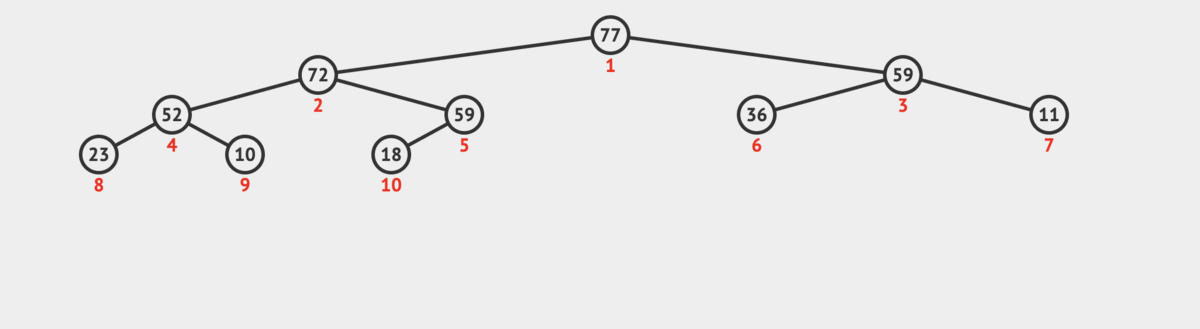
-
Pop the last element so we can bubble down the new root.
-
Heapify down the new root to its proper position:
- Compare the root to its left and right children
- Swap it with the larger child if necessary
- Repeat this process downwards until the heap property is satisfied
-
Once the new root is greater than its children or becomes a leaf, the heap property is satisfied.
The removal completes in O(log n) time since in the worst case we bubble/heapify down from the root to a leaf.
Applications of Heaps
Heaps are not just theoretical data structures; they have practical applications in a wide range of algorithms and problems:
1. Priority Queues
- Priority queues are a common use case for heaps.
- They allow efficient insertion of elements with associated priorities and quick retrieval of the element with the highest (or lowest) priority.
2. Heap Sort
- Heap Sort is a comparison-based sorting algorithm that uses a max-heap (or min-heap) to sort elements in ascending (or descending) order.
- It has a time complexity of
O(n log n), making it efficient for sorting large datasets.
3. Dijkstra’s Algorithm
- Dijkstra’s algorithm is used to find the shortest path in a weighted graph.
- It utilizes a min-heap to efficiently select the node with the shortest distance during each iteration.
4. Prim’s Algorithm
- Prim’s algorithm is used to find the minimum spanning tree of a connected, undirected graph.
- It also relies on a min-heap to select the edge with the lowest weight during each step.
Examples Problems
Median on streaming data
The heap can be used to calculate the streaming median. Python provides an inbuilt heapq implementation module.
Steps to calculate median
- Maintain two heaps:
- a max heap to store the smaller half of numbers
- a min heap to store the larger half.
- For each new number:
- Insert into either max heap or min heap based on the number value
- O(log n) for insertion
- After insertion, rebalance the heaps if needed:
- Insert into either max heap or min heap based on the number value
- To find the median:
- If heaps are equal in size, take an average of max of max heap and min of min heap
- O(1) since max and min are roots
- If unequal size, the median is in the larger heap
- O(1) to get the element at the root
- If heaps are equal in size, take an average of max of max heap and min of min heap
Overall runtime:
* Insertion of each element is O(log n)
* Getting the median is O(1)
By maintaining the balance between two heaps, we can efficiently calculate the median on streaming data. Heaps provide fast access to max and min elements needed for the median logic.
The overall process takes O(log n) per insertion making it efficient for large data streams.
import heapq
from typing import List
class MedianCalculator:
"""A class for calculating the median of streaming data using a min-max heap."""
def __init__(self):
"""Initialize the MedianCalculator."""
self.min_heap: List[int] = [] # Min-heap to store the larger half
self.max_heap: List[int] = [] # Max-heap to store the smaller half
def insert(self, num: int) -> None:
"""Insert a new element into the streaming data and update the heaps accordingly.
Args:
num: The new element to insert.
"""
if not self.max_heap or num <= -self.max_heap[0]:
heapq.heappush(self.max_heap, -num)
else:
heapq.heappush(self.min_heap, num)
# Balance the heaps
if len(self.max_heap) > len(self.min_heap) + 1:
heapq.heappush(self.min_heap, -heapq.heappop(self.max_heap))
elif len(self.min_heap) > len(self.max_heap):
heapq.heappush(self.max_heap, -heapq.heappop(self.min_heap))
def get_median(self) -> float:
"""Calculate and return the median of the streaming data.
Returns:
The calculated median.
"""
if len(self.max_heap) == len(self.min_heap):
return (-self.max_heap[0] + self.min_heap[0]) / 2
else:
return -self.max_heap[0]
if __name__ == "__main__":
median_calculator = MedianCalculator()
data_stream = [2, 5, 1, 8, 4, 7]
for num in data_stream:
median_calculator.insert(num)
median = median_calculator.get_median()
print(f"Median after inserting {num}: {median}")
Heap Sort
The heap can be used to sort an array in O(n log n) time.
Steps for Heap sort:
- We first convert the input list to a min-heap by pushing all elements into a heap. This takes
O(n)time. - Then we repeatedly pop the smallest element from the heap and append it to the sorted list. This takes
O(log n)time per pop. - By always removing the smallest element from the heap, we extract the elements in sorted order.
- Total runtime is
O(n + n log n) = O(n log n)since we donpops atO(log n)each.
from typing import List
import heapq
def heapsort(nums: List[int]) -> List[int]:
"""Sort the given list of numbers using the heapsort algorithm.
Args:
nums: Input array to sort.
"""
heap: List[int] = []
for num in nums:
heapq.heappush(heap, num)
sorted_nums: List[int] = []
while heap:
sorted_nums.append(heapq.heappop(heap))
return sorted_nums
if __name__ == "__main__":
nums = [5, 3, 1, 8, 0, 90, 2]
print(heapsort(nums)) # [0, 1, 2, 3, 5, 8, 90]